Desviación típica: aplicaciones prácticas y ejemplos de cálculo

Te ayudamos a elegir tu formación, pulsa aquí.

Máster en Técnicas Estadísticas + 60 Créditos ECTS

Online

1500h

60 ECTS

¡Me interesa!

Índice

Euroinnova APP

¡Aprender online está a solo un click!

Consíguelo en el

App Store

DISPONIBLE EN

Google Play

¿Qué es la desviación típica?

La desviación típica es una medida estadística que indica qué tan dispersos están los valores de un conjunto de datos con respecto a su media. En otras palabras, nos da una idea de cuánto se alejan los valores individuales del promedio.

Cuando los valores de un conjunto de datos tienen una desviación típica baja, significa que tienden a estar cerca del valor promedio. Por otro lado, si la desviación típica es alta, los valores están más dispersos alrededor de la media, lo que indica una mayor variabilidad en los datos. Quédate y descubre todos los detalles sobre qué es la desviación típica en estadística, cómo calcularla y qué mide la desviación típica. ¡Vamos!

¿Qué encontrarás aquí?

1. ¿Qué es la desviación típica?
1.1. Desviación típica y varianza
2. ¿Cómo se calcula la desviación típica S?
2.1. Fórmula de la desviación típica
2.2. Calcular desviación típica en Excel
3. Gráfico de distribución de la desviación típica
4. ¿Para qué sirve la desviación típica?
4.1. Ejemplo de desviación típica: cálculo paso a paso
5. ¿Cómo interpretar la desviación típica?
5.1. Diferencia entre la desviación estándar y desviación típica
6. Titulaciones que te pueden interesar

Desviación típica y varianza

La varianza y desviación típica son dos elementos muy relacionados. Para conocer cómo se calcula la desviación típica, es importante conocer qué es y cómo se calcula la varianza. ¡Veamos!

La desviación típica muestral o desviación típica de la muestra es simplemente la raíz cuadrada de la varianza de la muestra. Ambas son medidas de dispersión que describen cuánto se alejan los valores individuales de la media en un conjunto de datos. La desviación típica se prefiere comúnmente en la práctica debido a que su interpretación es más intuitiva y su relación directa con la escala de los datos originales. Sin embargo, la elección entre varianza y desviación típica puede depender de la situación y de los objetivos específicos del análisis.

La varianza se calcula tomando la diferencia entre cada valor y la media, elevando al cuadrado esa diferencia, sumando todos estos cuadrados y dividiendo por el número total de observaciones. La fórmula matemática de la varianza es la siguiente:

Donde:

son los valores individuales en el conjunto de datos.
$x ˉ$ es la media de los valores.
$n$ es el número total de observaciones.

Conocer la media y desviación típica de una muestra o conjunto de datos puede ser esencial para conocer datos reales y no quedarnos con la media de ellos. Imagina que el salario medio en una empresa es de 1.500 euros mensuales. Sin embargo, conocer la desviación típica nos permite saber qué tan dispersos se encuentran los salarios y, con ello, lo variables que son los sueldos. ¿Casi todos los trabajadores cobran 1.500 euros al mes o es que hay algunos trabajadores que, por ejemplo, cobran 3.000 y otros 500 euros?

¿Cómo se calcula la desviación típica S?

¿Quieres conocer el cálculo de la desviación típica S o $σ$ ? Descubre cómo hacer la desviación típica con su fórmula.

Fórmula de la desviación típica

La desviación típica ( $σ$ ) se obtiene al tomar la raíz cuadrada de la varianza:

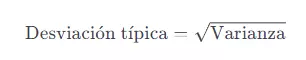
Fórmula desviación típica

Así pues, la desviación típica fórmula al completo luciría tal que así:

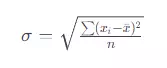
fórmula completa de desviación típica

Calcular desviación típica en Excel

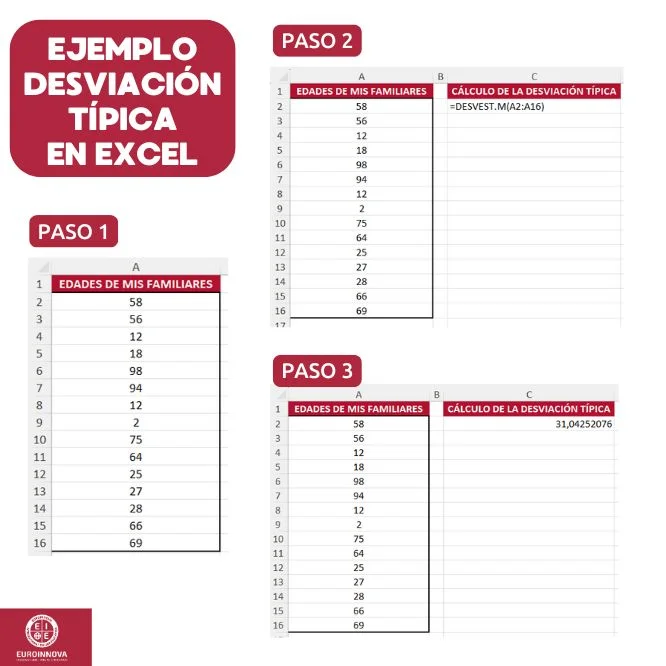
Una forma fácil de calcular la desviación típica es utilizar Excel. Gracias a la herramienta de desviación típica Excel, esta herramienta nos permite realizar el cálculo de forma rápida, simple y gráfica.

Para calcular la desviación típica con Excel, debes seguir los siguientes pasos:

Introduce el conjunto de datos en una columna de una nueva hoja de cálculo.
En una nueva celda, introduce la siguiente fórmula: DESVEST.M(A1:100). Recuerda que los valores del paréntesis deben coincidir con el rango de tus datos.
Dale a enter y obtendrás la desviación típica del conjunto de tus datos.

Te mostramos un ejemplo:

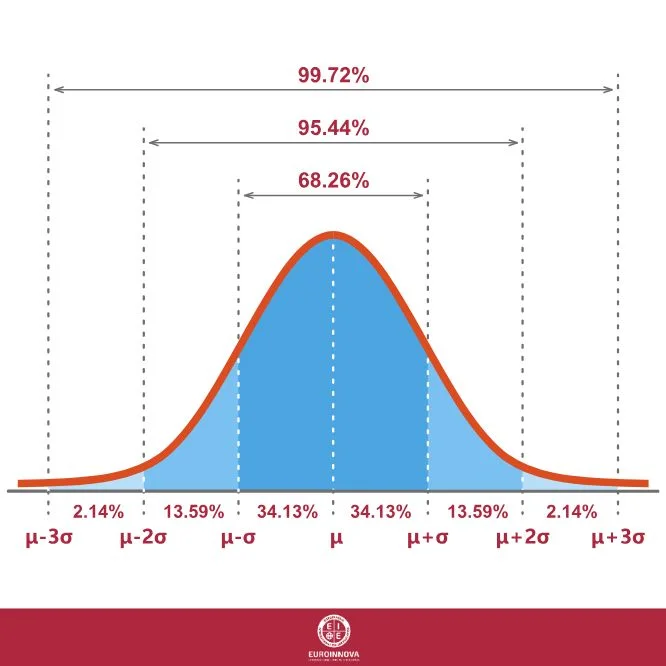
La gráfica típica para mostrar la distribución de la desviación típica es la campana de Gauss. Esta campana, también conocida como curva de distribución normal, es perfecta para mostrar gráficamente cómo funciona la desviación típica por varias razones:

La simetría refleja que los datos se distribuyen de manera simétrica alrededor de la media.
La mayor concentración en el centro corresponde a que la mayoría de los datos se agrupan cerca de la media.
Las desviaciones típicas a uno y otro lado de la media delimitan las regiones donde se concentra la mayor parte de los datos.

Aquí te dejamos el ejemplo del gráfico de distribución de la desviación típica.

alcular la desviación típica es útil en una variedad de situaciones prácticas para evaluar la dispersión o variabilidad de un conjunto de datos. Aquí tienes algunos ejemplos de usos prácticos de la desviación típica interpretación:

Finanzas: En el análisis financiero, la desviación típica se puede utilizar para medir la volatilidad de los rendimientos de una inversión y, con ello, tomar decisiones más óptimas. Un mayor valor de desviación típica indica mayor riesgo y variabilidad en los rendimientos.
Control de calidad: En la fabricación, la desviación típica se utiliza para evaluar la consistencia de los productos. Por ejemplo, en la producción de piezas mecánicas, una baja desviación típica indica que las dimensiones de las piezas son consistentes.
Meteorología: En el estudio del clima, la desviación típica se puede utilizar para analizar la variabilidad de las temperaturas a lo largo de un período de tiempo. Una mayor desviación típica sugiere que las temperaturas varían con mayor frecuencia.
Evaluación de rendimiento: En recursos humanos, la desviación típica se puede aplicar para evaluar la variabilidad en el rendimiento de los empleados en una empresa.

Ejemplo de desviación típica: cálculo paso a paso

¿Quieres conocer un desviación típica ejemplo? Supongamos que tenemos un conjunto de datos que representa las calificaciones obtenidas por un grupo de estudiantes en un examen, y queremos calcular la desviación típica para entender la variabilidad en estas calificaciones.

Conjunto de datos: ${85, 90, 88, 92, 87}$

Paso 1: Calcular la media ( $x ˉ$ ): Primero, sumamos todos los valores y luego dividimos por el número total de observaciones ( $n$ ):

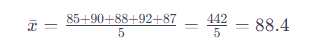
La media es 88.4.

Paso 2: Calcular las diferencias y sus cuadrados: Restamos la media (88,4) de cada calificación y elevamos al cuadrado estas diferencias:

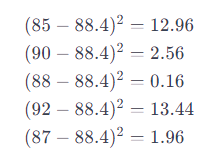
Paso 3: Calcular la varianza: Sumamos estos cuadrados y dividimos por el número total de observaciones ():

Paso 4: Calcular la desviación típica: Tomamos la raíz cuadrada de la varianza:

$σ = \sqrt 6.216 \approx 2.49$

Interpretación: La desviación típica es aproximadamente $2,49$ . Esto significa que, en promedio, las calificaciones de los estudiantes tienden a desviarse alrededor de 2,49 puntos de la media ( $88,4$ ). Una desviación típica más baja indica que las calificaciones están más cercanas entre sí, mientras que una desviación típica más alta indica una mayor dispersión en las calificaciones. En este caso, $2,49$ puntos podrían considerarse como una variabilidad moderada en las calificaciones de los estudiantes.

¿Cómo interpretar la desviación típica?

La desviación típica es una medida de dispersión que indica cuánto se alejan, en promedio, los valores individuales de un conjunto de datos respecto a su media. En términos generales, la interpretación de la desviación típica se puede interpretar de dos maneras:

Cuando la desviación típica es pequeña, significa que la mayoría de los valores están cercanos a la media. Por tanto, los datos tienden a ser más homogéneos y consistentes. Por otra parte, una desviación típica grande indica que los valores están más dispersos alrededor de la media. En este caso, los datos son más heterogéneos y muestran una mayor variabilidad.

Diferencia entre la desviación estándar y desviación típica

Para terminar con todo lo que debes saber sobre la desviación típica, es importante que aprendas la diferencia entre la desviación estándar y la desviación típica. ¿Vamos?

Te lo ponemos fácil: no existe ninguna diferencia. Realmente, la desviación estándar y la desviación típica son dos denominaciones de un mismo concepto estadístico, por lo que no existe diferencia entre ellas. El primero es un término más común en Latinoamérica y, el segundo, en España.

Puede que te interese leer sobre: