Índice
El teorema de Tales, uno de los pilares fundamentales de la geometría, tiene una fascinante historia que se remonta a la antigua Grecia y Egipto. Este artículo explorará cómo Tales de Mileto aplicó ingeniosamente su teorema para calcular la altura de las pirámides egipcias, un logro que ha perdurado en la historia de las matemáticas.
Tales de Mileto, considerado uno de los Siete Sabios de Grecia, viajó a Egipto en el siglo VI a.C. y se encontró frente a las majestuosas pirámides de Guiza. Fascinado por estas estructuras colosales, Tales se propuso medir la altura de la Gran Pirámide de Keops, un desafío aparentemente imposible sin escalarla directamente.
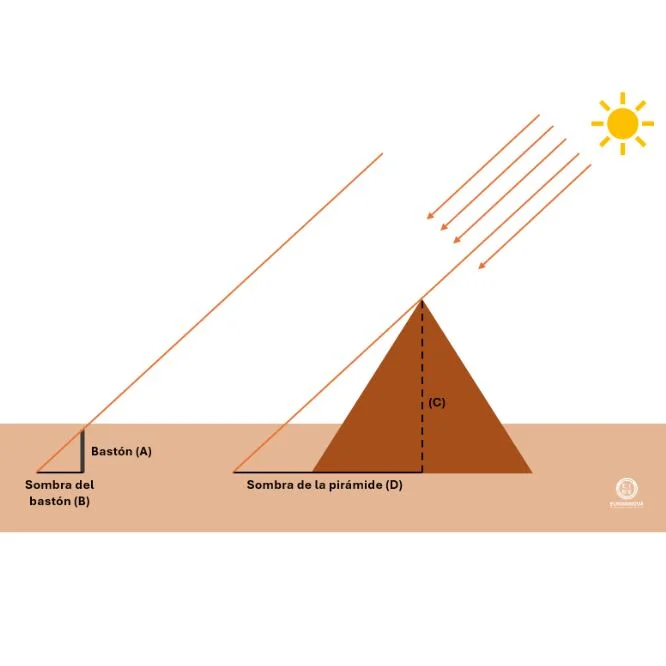
Para conseguirlo, Tales ideó un método ingenioso basado en la observación de las sombras. Esperó hasta el momento del día en que la longitud de la sombra de un objeto era igual a su altura real. En ese preciso instante, Tales clavó su bastón verticalmente en la arena y midió su sombra. Aplicando el principio de proporcionalidad que más tarde se conocería como el teorema de Tales, estableció que la relación entre la altura de su bastón y la longitud de su sombra sería la misma que la relación entre la altura de la pirámide y la longitud de su sombra. Esta brillante deducción le permitió calcular la altura de la pirámide sin necesidad de utilizar más herramientas.
El teorema de Tales establece que, si una línea paralela corta dos rectas, los segmentos determinados en una de las rectas son proporcionales a los segmentos correspondientes en la otra. En el caso de la pirámide, Tales consideró los rayos del sol como líneas paralelas que formaban dos triángulos semejantes: uno con su bastón y su sombra, y otro con la pirámide y su sombra.
La fórmula matemática que representa este principio es:
Para ilustrar cómo Tales pudo haber realizado el cálculo, consideremos un ejemplo numérico:
Supongamos que:
Aplicando la fórmula del teorema de Tales:
El método de Tales para medir la altura de la pirámide no solo demostró la aplicabilidad práctica de los principios geométricos, sino que también sentó las bases para futuros desarrollos en trigonometría y cálculo de distancias inaccesibles. Su aplicación se encuentra en diversos campos.
Por ejemplo, en arquitectura, se utiliza para calcular la altura de edificios y estructuras, permitiendo a los ingenieros diseñar rascacielos y puentes con precisión. En la industria de la construcción, ayuda a determinar la inclinación adecuada de techos y escaleras. Los topógrafos lo emplean para medir distancias y alturas en terrenos irregulares, facilitando la creación de mapas precisos.
En la navegación, tanto marítima como aérea, el teorema es fundamental para calcular distancias a puntos de referencia inaccesibles. Los astrónomos lo aplican para estimar el tamaño y la distancia de cuerpos celestes. En la tecnología moderna, se utiliza en el diseño de lentes para cámaras y telescopios, así como en sistemas de posicionamiento global (GPS). Incluso en el arte, los pintores y escultores lo emplean para crear perspectivas realistas y proporciones adecuadas en sus obras.
La historia de Tales y la medición de las pirámides es un testimonio del poder del pensamiento lógico y la observación cuidadosa. Su método, basado en el teorema que lleva su nombre, sigue siendo relevante en la actualidad, no solo en geometría sino también en campos como la arquitectura, la ingeniería y la astronomía.
El legado de Tales nos recuerda que las matemáticas no son solo abstracciones, sino herramientas poderosas para comprender y medir nuestro mundo. Su ingenio al enfrentarse al desafío de las pirámides egipcias continúa inspirando a estudiantes y matemáticos, demostrando que, con creatividad y razonamiento lógico, incluso los problemas más intimidantes pueden ser resueltos.
Quizá te interesa leer sobre...
Marta Ester Lopez Viseras
DOCENTE DE LA FACULTAD DE CIENCIAS
¡Muchas gracias!
Hemos recibido correctamente tus datos. En breve nos pondremos en contacto contigo.
-1652067351.webp "Enterate de cuánto dura la carrera de Química")
