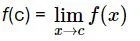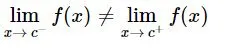Continuidad y límites: todo lo que debes saber

Un límite es un concepto fundamental en el cálculo y el análisis matemático que describe el comportamiento de una función cuando la variable independiente se aproxima a cierto valor, ya sea finito o infinito.

Los principios fundamentales de los límites y la continuidad en el contexto de una función real son esenciales en el análisis matemático, ya que proporcionan las herramientas necesarias para examinar en profundidad las propiedades y formas de dichas funciones.

¿Para qué sirve el análisis matemático a partir de los límites y la continuidad?

Este análisis sirve como base para definiciones clave en matemáticas, como las derivadas e integrales de funciones, las cuales tienen una importancia crucial en diversos campos como la física, la economía y otros, donde se aplican para calcular velocidades, aceleraciones, costos marginales y más.

Más formalmente, se dice que el límite de una función f(x) cuando x tiende hacia a es L, denotado como:

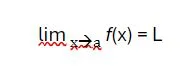
Esto significa que cuando los valores de x se acercan al valor a, los valores correspondientes de f(x) se acercan a L. Sin embargo, es importante destacar que el valor de la función en a en sí no necesita estar definido o ser igual a L para que el límite exista. Lo que importa es el comportamiento de la función en las proximidades de a.

Límites laterales

Para seguir avanzando en este concepto, vamos a hablar primero de los límites laterales:

Límite lateral por la izquierda: Este límite se denota como y describe el comportamiento de la función a medida que x se aproxima a a desde valores menores que a. En otras palabras, examina cómo se comporta la función cuando nos acercamos al punto a moviéndonos desde valores menores que a en el eje x.

Límite lateral por la derecha: Este límite se denota como y describe el comportamiento de la función a medida que x se aproxima a a desde valores mayores que a. Se refiere a cómo se comporta la función cuando nos acercamos al punto a moviéndonos desde valores mayores que a en el eje x.

¿Cuándo no existe el límite de una función en un punto?

Existen diferentes condiciones que hacen que un límite no exista, pero vamos a ver las dos más sencillas.

La primera condición para que exista el límite de f(x) en un punto es que la función esté definida en ese punto.

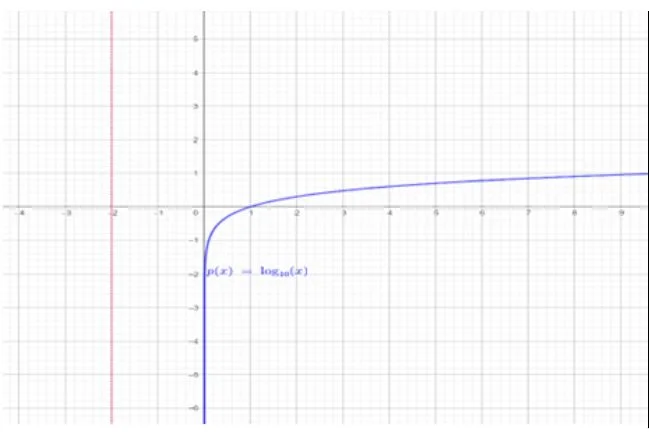
En esta primera función tenemos que Dom p(x) = (0, ∞), por tanto, tendremos que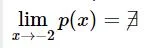 

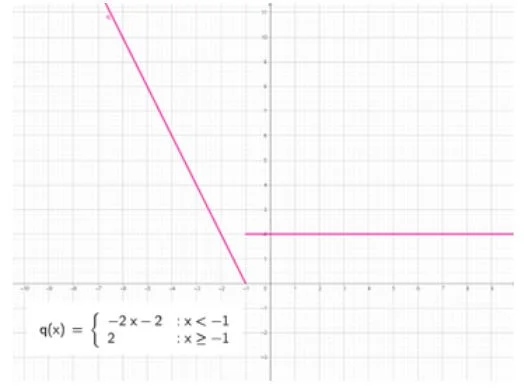
Otra de las condiciones para que exista el límite de una función en un punto es que los límites laterales coincidan. Por ejemplo, en la siguiente función definida a trozos tenemos que:

[Ecuación]

Como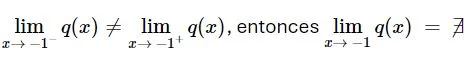

Concepto de continuidad

Conociendo esto podemos entrar en el concepto de continuidad. Por definición, una función es continua en un punto si el valor del límite en ese punto coincide con el valor de la función, es decir:

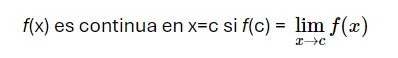
Según lo que hemos visto antes, para que una función f(x) sea continua en x=a se tiene que cumplir que:

1. La función está definida en c.
2. El límite de la función cuando x tiende a c existe, es finito y coincide con el valor de la función en c. Es decir, 
3. Los límites laterales de la función cuando x se aproxima a c desde ambos lados existen y son iguales, lo que significa que 

Vamos a ver un ejemplo:

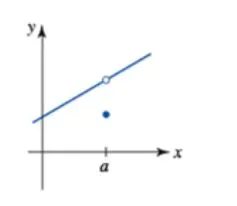
En esta función los límites laterales cuando x tiende al punto a son iguales, pero difieren del valor de la función en ese punto, por tanto, no es continua en x = a.

De una manera más fácil se dice que la continuidad de una función implica que su gráfico no tiene quiebres ni saltos, sino que se puede dibujar sin levantar el lápiz, formando una curva suave y continua. Esta propiedad es esencial en matemáticas y ciencias aplicadas, ya que permite modelar fenómenos de manera más precisa y realizar cálculos y análisis de manera más rigurosa.

La importancia de los límites y la continuidad

En conclusión, espero que hayas comprendido estos conceptos básicos del cálculo diferencial: los límites y la continuidad son pilares fundamentales que sustentan el análisis matemático y tienen aplicaciones extendidas en diversas disciplinas.

Al dominar estos conceptos, estarás preparado para abordar de manera más sólida y precisa problemas complejos en matemáticas y campos relacionados. Si quieres profundizar más en estos temas y explorar sus aplicaciones en profundidad, te invito a que no te pierdas nuestro Curso de Cálculo Diferencial.

Quizá te interesa leer sobre...

• Límites por definición
• ¿Qué es una función lineal y cómo se representa?
• Juegos de matemáticas para Secundaria y Bachillerato

Formaciones que te pueden interesar

• Máster en ingeniería matemática
• Curso de Cálculo diferencial de las Ciencias Económicas