Descubre qué es una función lineal y cómo se representa

En matemáticas las funciones determinan el tipo de relación que guardan dos elementos o variables entre sí. Por lo tanto, son muy útiles para describir fenómenos, en especial, en áreas como las finanzas, estadísticas, ingeniería, medicina, economía, entre otros. Hoy queremos dedicarnos este artículo a hablar sobre qué es una función lineal y cómo se representa, además de abordar terminología básica como función lineal en álgebra, cálculo lineal, entre otros. Así que te invitamos a leerlo si este tema es de tu interés.

Para aclarar tus dudas, hemos preparado este artículo. Quédate con nosotros y aprende sobre qué es y la importancia de la función lineal.

¿Qué es una función lineal y cómo se representa?

Esta es la definición de función lineal. Dentro de la geometría analítica y álgebra, se conoce como una función polinómica en primer grado que se representa de la siguiente forma:

Función lineal fórmula → f (x) = m ⋅ x + b

Si analizamos la expresión o fórmula lineal, vemos como al tener el valor de  x, lo primero que debe hacerse es multiplicarlo por m y el producto sumarlo a b. Por lo tanto, el resultado de toda esta operación será el valor de f de x (f (x)).

Las funciones lineales son muy útiles para el cálculo de fenómenos que ocurren en la vida cotidiana. Por ejemplo, el costo de los servicios básicos como el agua, la luz o el gas, pueden ser determinados a través de esta función. Además del monto, será posible tener en cuenta la proporción en los casos de aumentos.

La función lineal características que pueden mencionarse son:

• Su representación en el plano cartesiano corresponde a una línea recta (razón por la que se le conoce como función lineal).
• m representa un valor de cambio, mientras que b es una constante.

Con esto, es posible responder a qué es una función lineal en matemáticas.

Elementos de la función lineal

Atendiendo a su forma de expresión f (x) = m ⋅ x + b, los elementos que la integran son:

• x: variable independiente (su valor no depende de ninguna otra variable y puede ser asignado libremente).
• f (x): en algunos casos es representada con el símbolo y. Corresponde a la variable dependiente (su valor depende de x).
• m: se refiere a la pendiente, la cual determina el grado de inclinación de la recta.
• b: se conoce como origen y corresponde al corte de eje.

Formas de representación de la función lineal

La función algebraica representación gráfica se describe a continuación. Como vimos a través de una expresión o fórmula sirve para representar una función lineal, sin embargo, este proceso también es posible a través de una tabla o un gráfico.

Para dejar más en claro qué es una función lineal y cómo se representa, vayamos a un ejemplo.

Tabla

Tenemos la siguiente función:  f (x) = 2x + 0

Según esta fórmula es posible determinar cuál tabla y valores deben registrarse.

Aquí, los valores de x fueron designados de forma arbitraria, mientras que los de y se originaron a partir del cálculo de una ecuación lineal:

y = m ⋅ x

De modo que, el primer valor se calcula a partir de la multiplicación de m= 2 por x = 0.

y = 2 ⋅ 0

= 0

Mientras que el segundo se calcula por m = 2 por x = 2. Quedan así:

y = 2 ⋅ 2

= 4

Al fijarnos en la tabla y en la operación vemos como los valores representan puntos que pueden estar en el plano cartesiano.

Representación cartesiana

Para las gráficas lineales, tomamos los valores (x, y) plasmados en la tabla, o los obtenidos a través de la operación y representamos.

A = (0,0)

B = (2,4)

C = (4,8)

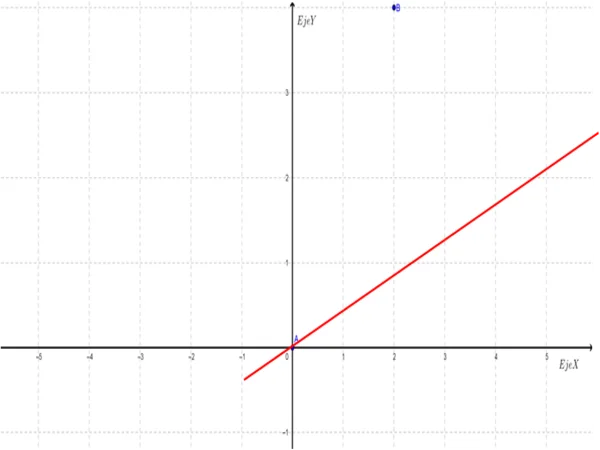
Como vemos, se forma una recta lineal con crecimiento proporcional, lo que quiere decir, que se trata de una función constante donde el aumento de valor de X, es proporcional al valor de Y.

Al igual que cada aspecto de las matemáticas, las funciones lineales son aplicables en la realidad. Por eso, te invitamos a formarte en lo que sería una escuela especializada en negocio, donde podrás aprender sobre este y otros temas relacionados.

Ejemplos de función lineal

Veamos, a continuación, ejemplos de funciones lineales. Presentamos dos casos: una función lineal creciente y una función lineal decreciente. 

Ejemplo de función lineal creciente

Vamos a tomar este supuesto para realizar el ejemplo de función lineal. Partimos de la premisa de que, debido a factores como la baja producción de olivo y la alta demanda del producto, el precio del aceite de oliva extra virgen tenido un incremento considerable en los principales centros de abasto, como comercios de barrio, supermercados, entre otros. Para explicar este caso, vamos a observar el aumento de este precio desde 2024 hasta 2034. 

Sabemos que la función lineal tiene la siguiente forma: 

f(x)= m ⋅ x +b 

Como vimos, m representa a la pendiente o el cambio en el valor de f(x) por cada unidad de x. En nuestro caso, el incremento estará sujeto a la inflación. A su vez, b es el valor inicial, donde nosotros tomamos como referencia el precio del aceite en 2024. Por último, x es la variable independiente, es decir, los años transcurridos desde el año base. 

Paso 1. Establecer los datos iniciales 

Entonces, podemos decir que los datos iniciales son los siguientes: 

• Precio base en 2024: 10 euros por litro (b=10) 

• Inflación anual referencial: 3 % (m = 0.03 ⋅ 10 = 0.3) 

• Variable: número de años desde 2024 (x) 

Paso 2. Escribir la función lineal 

El siguiente paso es escribir la función lineal: 

f(x) = 0.3 ⋅ x +10, ya que 

• f(x) es el precio de aceite en euros después de x años 

• x es el número de años transcurridos 

Paso 3. Calcular los precios 

Como siguiente paso se calcula el precio en distintos años para ver cómo afecta la inflación a este producto- 

En 2024 (x = 0) 

f(o) = 0.3 ⋅ 0 + 10 euros 

En 2025 (x = 1) 

f(1) = 0.3 ⋅ 1 + 10 euros  = 10.3 euros

En 2026 (x = 2) 

f(2) = 0.3 ⋅ 2 + 10 euros = 10.6 euros

En 2030 (x = 6) 

f(6) = 0.3 ⋅ 6 + 10 euros = 11.8 euros

Paso 4. Graficar la función

La gráfica de la función es la siguiente:

Ejemplo de función lineal decreciente

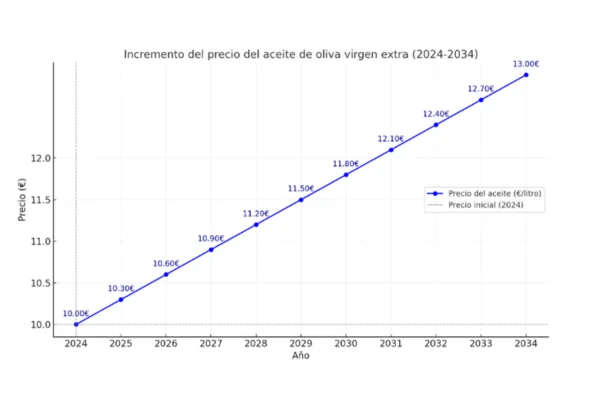
Ahora vamos a construir una función lineal decreciente que modela la reducción en las ventas de botellas de aceite de oliva virgen extra de 1 litro en los 12 meses que componen el año 2024. Tomamos como base el aumento de precio causado por la inflación.

Recordemos que la función lineal decreciente posee esta forma:

f(x)=−m ⋅ x + b

Sabemos que m corresponde a la pendiente, que tiene que ver con la disminución en las ventas de botellas por cada euro que sube el precio. El signo negativo que antecede a m, en este caso, indica que la función decrece. No olvidemos que b es el valor inicial o constante, es decir, la cantidad de botellas vendidas cuando el precio no varía. Por último, x es la variable independiente, es decir, el incremento del precio respecto del precio base.

Paso 1. Establecer los datos iniciales

• Precio base del aceite de oliva: 10 euros por litro
• Incremento mensual en el precio: 0.3 € por mes (3% anual dividido en 12 meses)
• Ventas estimadas al precio base: 1000 botellas por mes
• Reducción en ventas por cada euro de aumento: 50 botellas menos por euro de aumento (m = 50)

Paso 2. Escribir la función lineal decreciente

• Precio mensual

El precio aumenta 0.3 € cada mes. La función para el precio mensual es:

Precio(m) = 10 + 0.3  ⋅m

Donde m es el número del mes (m = 0 para enero, m = 1 para febrero, y así sucesivamente).

• Ventas mensuales

A medida que sube el precio, las ventas disminuyen. La función para las ventas mensuales es:

Ventas(m) = −50 ⋅ (Precio(m) − 10) + 1000

Donde:

Precio(m) − 10 es el incremento en el precio respecto al precio base.

Paso 3. Calcular los precios y las ventas

Ahora se calculan los precios y las ventas para cada mes de 2024.

Paso 4. Elaborar el gráfico

Esta es la gráfica de función lineal:

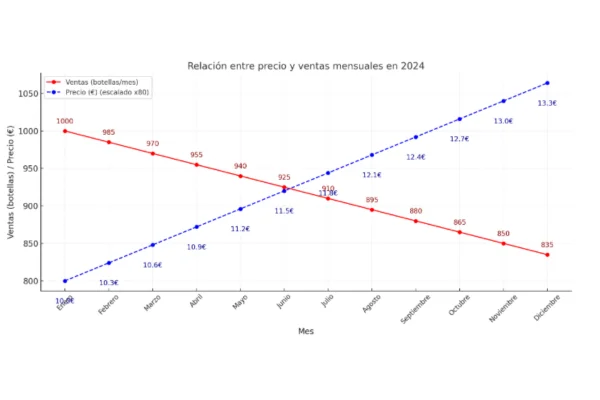
Como vemos, la línea roja representa la disminución de las ventas, mientras que la línea azul, la escalada de los precios.

Titulaciones que te pueden interesar

Profundiza tus conocimientos sobre qué es una función lineal y cómo se representa  con la oferta formativa que ponemos a tu disposición:

• Máster en Técnicas Estadísticas
• Máster en Estadística Aplicada
• Curso en Estadística Avanzada en Ciencias de la Salud