Índice
En el ámbito de las matemáticas, las fracciones representan partes de un todo, permitiendo cuantificar y comparar con precisión diversas magnitudes. La resta de fracciones, por su parte, surge como una operación fundamental para determinar la diferencia entre dos o más cantidades fraccionarias.
Este artículo tiene como objetivo principal abordar la resta de fracciones de manera clara, concisa y práctica. A través de un lenguaje sencillo y ejemplos ilustrativos, se busca guiar al lector en el dominio de esta operación matemática esencial.

La resta de fracciones -también denominada sustracción de fracciones- implica encontrar la diferencia entre dos o más cantidades fraccionarias. Para realizarla de manera efectiva, es necesario considerar si las fracciones tienen el mismo denominador, es decir, la parte inferior que representa la unidad que se divide.
En otras palabras, la resta de fracciones es una operación matemática fundamental que permite cuantificar la diferencia entre dos o más cantidades fraccionarias. Su dominio es esencial para el desarrollo de habilidades numéricas y la resolución de problemas en diversos contextos.
Ten en cuenta que existen distintos tipos de restas de fracciones: desde restas de fracciones homogéneas (mismo denominador) hasta restas de fracciones heterogéneas (distintos denominadores), restas de fracciones equivalentes, y mucho más... Entender que cada una de ellas puede seguir un procedimiento distinto es esencial.
Cuando las fracciones a restar comparten el mismo denominador, la operación se simplifica considerablemente. En este caso, solo se requiere restar los numeradores (la parte superior que indica la cantidad de unidades) y mantener el denominador común.

Una de las operaciones con fracciones heterogéneas (distinto denominador) más frecuente son las restas.
Si las fracciones a restar tienen distinto denominador, es necesario encontrar un mínimo común múltiplo (MCM) para ambas fracciones. El MCM es el número más pequeño que es múltiplo de ambos denominadores. Una vez hallado el MCM, se procede a:
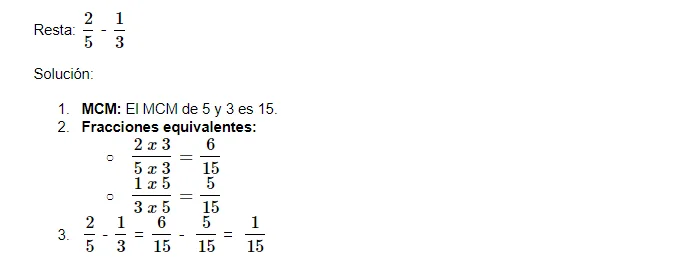
Las fracciones con denominadores coprimos son aquellas que no tienen ningún factor común aparte del 1. Es decir, son fracciones que no son divisibles por ningún otro número que no sea 1.
Por ejemplo: las fracciones 1/2 y 1/3 son coprimas porque su único divisor común es 1, mientras que las fracciones 1/3 y 1/6 no lo son porque, además del 1, ambas son divisibles por 2.
Y: ¿Cómo se hace una resta de fracciones con denominadores coprimos?

Otro ejemplo de resta de fracciones es la de fracciones con un denominador que es divisor del otro. Es decir, fracciones en las que el "denominador pequeño" es un divisor exacto del "denominador grande", sin restos.
Un ejemplo de fracciones con un denominador que es divisor de otro sería: 3/4 y 5/8, pues el 4 es divisor exacto de 8, sin dejar restos (8 ÷ 4 = 2).
En este caso, ¿cómo se hace la resta de fracciones con un denominador que es divisor de otro? ¡Aquí no es necesario multiplicar los denominadores, sino llevar la fracción más pequeña al denominador mayor!

Para reforzar la comprensión de la resta de fracciones, se presentan a continuación algunos ejercicios de restas de fracciones resueltos:

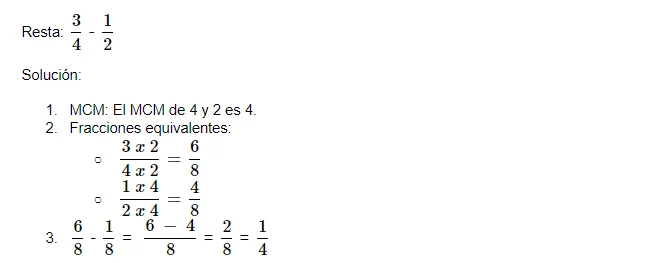
A continuación, se presenta un ejemplo de problemas de fracciones de resta con su respectiva resolución:
María tiene 3/4 de litro de jugo de naranja y consume 1/2 litro. ¿Qué cantidad de jugo le queda?
Solución:
Cantidad de jugo restante = Cantidad inicial - Cantidad consumida


Para fortalecer el aprendizaje de la resta de fracciones, se sugieren las siguientes recomendaciones:
Para facilitar la resolución de problemas de resta de fracciones, se sugieren las siguientes estrategias:
Visualizar las fracciones: Utilizar diagramas, círculos o rectángulos divididos en fracciones para representar las cantidades involucradas en el problema.
Plantearse preguntas guía: Formular preguntas como: ¿Qué cantidad se resta? ¿Qué fracción queda? ¿Cómo se relaciona la diferencia con las fracciones iniciales?
Descomponer las fracciones: En algunos casos, descomponer las fracciones en denominadores comunes más pequeños puede simplificar la operación.
Utilizar recursos matemáticos: Emplear calculadoras o software educativo que permitan realizar operaciones con fracciones.
Quizá te interesa leer sobre:
¿Quieres conocer más sobre la adición y sustracción de fracciones heterogéneas y homogéneas? ¡Fórmate online en matemáticas!


¡Muchas gracias!
Hemos recibido correctamente tus datos. En breve nos pondremos en contacto contigo.