Índice
Las asíntotas de una función son un concepto muy importante en el análisis matemático que nos ayuda a comprender el comportamiento de las funciones en el infinito o cerca de puntos donde la función no está definida. El estudio de las asíntotas de una función sirve para visualizar y analizar gráficas de funciones complejas, y tiene aplicaciones en diversos campos como la física, la ingeniería y la economía.

Las asíntotas de una función son líneas rectas a las que la gráfica de la función se aproxima indefinidamente sin llegar a tocarlas o cruzarlas. En otras palabras, la distancia entre la función y la asíntota tiende a cero cuando la función se aproxima al punto en el que se encuentra la asíntota. Existen tres tipos principales de asíntotas de una función: verticales, horizontales y oblicuas.
Para realizar las explicaciones necesarias en el resto del artículo, utilizaremos los ejes cartesianos, siendo y el eje de ordenadas y x el eje de abscisas.
Las asíntotas verticales son líneas rectas verticales a las que la gráfica de la función se aproxima cuando la variable independiente x se acerca a un valor específico, ya sea por la izquierda o por la derecha. Estas asíntotas ocurren cuando la función tiende a infinito (positivo o negativo) mientras x se acerca a un valor a determinado, es decir, cuando se cumple alguna de estas dos condiciones:
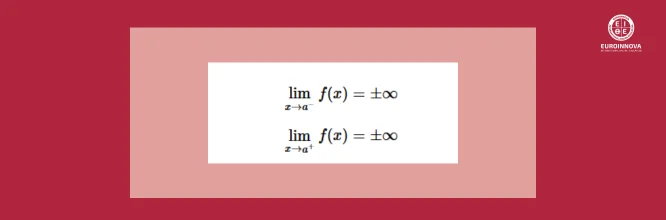
El superíndice + o – en a indica que x se aproxima a a por la izquierda o por la derecha, respectivamente. La asíntota vertical se representa con la recta x = a.
En una función racional, las asíntotas verticales están en los valores de x que hacen que el denominador de la función sea cero, siempre que el numerador no se anule simultáneamente. Por ejemplo, en la función:
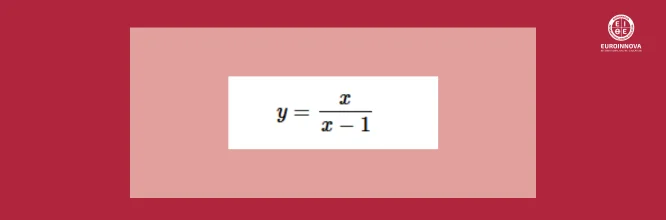
hay una asíntota vertical en x = 1
Otro ejemplo de función con asíntotas verticales es la función tangente. En este caso, tiene infinitas asíntotas verticales. En la siguiente figura hemos representado en y = tan x en color verde, y podemos comprobar que tiene asíntotas (azules) en
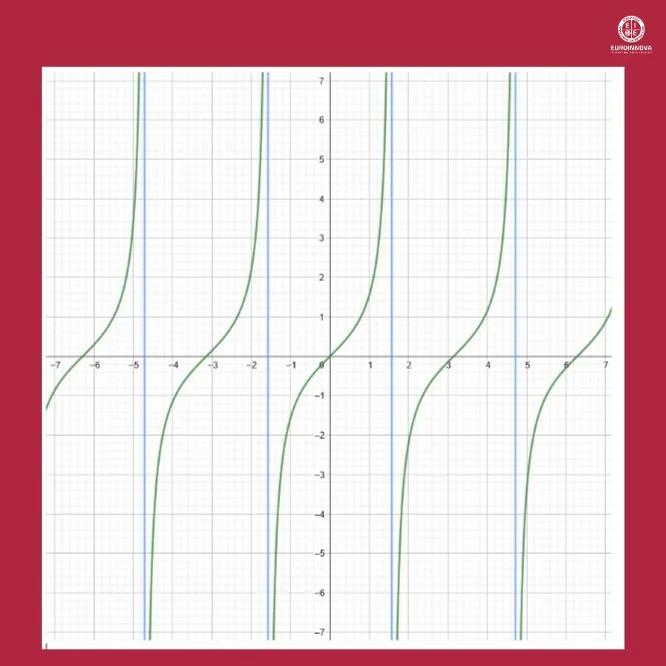
Las asíntotas horizontales son líneas rectas horizontales a las que la gráfica de la función se aproxima cuando la variable independiente x tiende a infinito positivo o negativo. Estas asíntotas nos dan información sobre el comportamiento de la función para valores muy grandes o muy pequeños de x. La condición para que exista una asíntota vertical es:
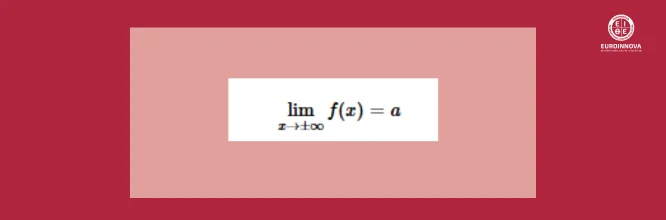
Si este límite existe siendo a un número finito, tendremos una asíntota horizontal, representada por la recta y=a.
Siguiendo con el ejemplo anterior, tenemos que la función:

tiene una asíntota horizontal en y=1.
Podemos ver la función anterior, con sus asíntotas vertical y horizontal, en la siguiente figura:
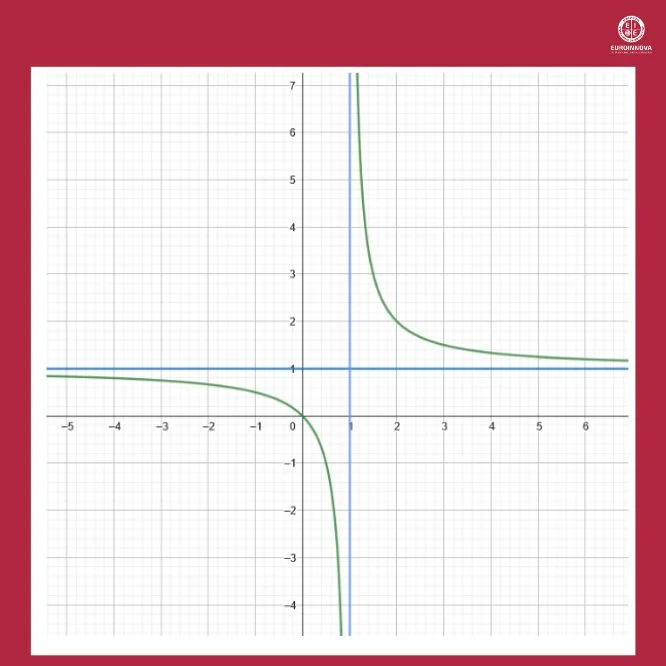
Las asíntotas oblicuas son rectas no horizontales ni verticales a las que la gráfica de la función se aproxima cuando x tiende a infinito. Estas asíntotas son particularmente interesantes porque nos dan información sobre el comportamiento de la función para valores muy grandes de x, incluyendo tanto la pendiente como la intersección con el eje y.
Calcular una asíntota oblicua es más complejo que calcular las asíntotas verticales y horizontales. Para que la recta y=mx + b sea una asíntota oblicua, debe cumplirse que m ≠ 0 y, además:

Dicho de otro modo, si hacemos la resta de la función original menos la función que representa la asíntota, tendremos una asíntota horizontal en y=0. Los valores de m y b se calculan con las siguientes fórmulas:

Aquí puedes comprobar la representación:
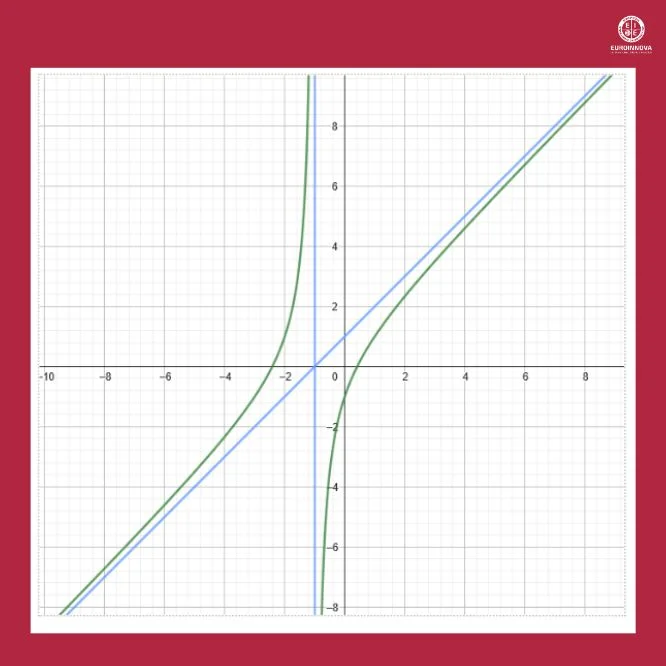
El concepto de asíntota de una función tiene numerosas aplicaciones en matemáticas y ciencias aplicadas. Por ejemplo, en física, las asíntotas pueden describir el comportamiento límite de sistemas físicos, como la velocidad terminal de un objeto en caída libre. En economía, las asíntotas pueden representar límites de producción o consumo en modelos económicos.
Para dominar el cálculo de asíntotas, es necesario practicar con una variedad de ejercicios que abarquen diferentes tipos de funciones y situaciones. Los ejercicios de asíntotas suelen incluir:
Al resolver estos ejercicios, es importante seguir un enfoque sistemático:
En este post sobre Asíntotas para Selectividad se puede comprobar cómo se sigue este enfoque sistemático en los distintos ejercicios que se proponen.
El estudio de las asíntotas de una función es un tema fundamental en el análisis matemático. Comprender cómo calcular y analizar asíntotas verticales, horizontales y oblicuas nos permite obtener información valiosa sobre el comportamiento de las funciones en situaciones extremas o cerca de puntos críticos.
La práctica constante con ejercicios variados es vital para dominar el cálculo de asíntotas. A medida que se gana experiencia, se desarrolla la intuición para identificar rápidamente los tipos de asíntotas presentes en una función y se mejora la capacidad de interpretar su significado en contextos aplicados.
Las asíntotas de una función no solo son un concepto matemático abstracto, sino una herramienta poderosa para modelar y analizar fenómenos del mundo real. Su aplicación en campos como la física, la ingeniería y la economía demuestra la importancia de este concepto más allá del ámbito puramente matemático.
En resumen, el dominio de las asíntotas de una función, incluyendo el cálculo de asíntotas verticales, horizontales y oblicuas, así como la resolución de ejercicios relacionados, es una habilidad esencial para cualquier estudiante o profesional que trabaje con análisis matemático y sus aplicaciones.
Si quieres recibir formación especializada en temas relacionados con análisis de funciones, puedes realizar el Curso de Cálculo Diferencial que ofrece Euroinnova, en el que puedes profundizar en varios de los conceptos que hemos visto en este artículo.
Quizá te interesa leer sobre...

¡Muchas gracias!
Hemos recibido correctamente tus datos. En breve nos pondremos en contacto contigo.