Índice
Al observar la Naturaleza, nos percatamos de que muchos procesos físicos, como la rotación de la tierra en torno al eje polar, se repiten regularmente, sucediendo los eventos de manera cíclica después de un intervalo de tiempo constante. En tales casos, nos referimos al movimiento como periódico, y lo caracterizamos por su período, que es el tiempo requerido para completar un ciclo del movimiento, o su frecuencia, que representa el número de ciclos completos por unidad de tiempo.

Un caso de movimiento periódico interesante ocurre cuando un sistema físico oscila alrededor de una posición de equilibrio estable. Este sistema sigue una trayectoria idéntica, primero en una dirección y luego en la dirección opuesta, cambiando el sentido de su movimiento en los extremos de la trayectoria. Un ciclo completo comprende pasar dos veces por la posición de equilibrio. Ejemplos de sistemas físicos que a menudo exhiben este tipo de movimiento oscilatorio incluyen la masa en el extremo de un péndulo o un resorte, la carga eléctrica almacenada en un condensador, las cuerdas de un instrumento musical y las moléculas en una red cristalina.
El movimiento oscilatorio más simple se conoce como movimiento armónico simple, el cual ocurre cuando la fuerza resultante que actúa sobre el sistema es una fuerza restauradora lineal. Siendo uno de los fenómenos más comunes en la física, y mejor vistos en Introducción a la Física.
Una de las casuísticas más habituales es la de tener una mas unida a un muelle. Se toman como simplificaciones habituales las de eliminar la masa del muelle, reducir a 0 el rozamiento con el aire, y para los primeros ejercicios también se elimina el rozamiento de la masa con la superficie.
Supongamos entonces que el movimiento se realiza sobre una superficie horizontal de manera unidimensional y sin rozamiento. La posición inicial la denominamos como x = 0. La fuerza que ejerce el muelle varía en función de la posición de la masa. Esta fuerza viene definida por la Ley de Hooke
Fs= -kx
Donde k es la constante, mayor a cero, de recuperación del muelle. Y x indica la posición de la masa.
El Teorema de Fourier proporciona una justificación de la relevancia del fenómeno del movimiento armónico simple. De acuerdo con este teorema, cualquier forma de movimiento periódico u oscilatorio puede ser conceptualizada como la composición de movimientos armónicos simples.
La ley de Hooke representa únicamente una aproximación lineal de primer orden a la respuesta real exhibida por resortes y otros cuerpos elásticos frente a las fuerzas aplicadas. En última instancia, esta aproximación está destinada a perder validez una vez que las fuerzas superen cierto umbral, dado que ningún material puede ser comprimido más allá de un límite mínimo o estirado más allá de un límite máximo sin experimentar alguna forma de deformación permanente o cambio de estado. Es importante destacar que muchos materiales mostrarán desviaciones significativas respecto a la ley de Hooke mucho antes de alcanzar estos límites elásticos mencionados.

Al fin y al cabo una fuerza es expresable como masa por aceleración. Por lo que podemos escribir:
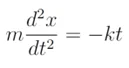
Donde hemos sustituido la aceleración por la segunda derivada de la posición respecto del tiempo. Despejando la aceleración, tenemos:
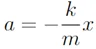
Que podemos reescribir como
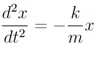
Definimos una nueva constante, ω, como
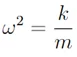
Que al sustituirlo en la expresión anterior nos queda como
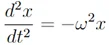
Para más comodidad podemos despejar en ambas ecuaciones los términos, para dejarlos en el mismo miembro de la ecuación.
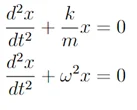
Para saber más sobre este tipo de desarrollo, no dudes en ver Especialista en Cálculo
Estas ecuaciones diferenciales de segundo orden dan la siguiente función coseno como solución,
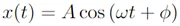
Donde A es la amplitud del movimiento, es decir, el valor máximo de la posición tanto en la zona positiva como negativa. Y 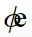 es el ángulo de la fase.
es el ángulo de la fase.
En la siguiente imagen vemos la gráfica de un movimiento oscilatorio con amplitud igual a uno; y posición inicial 0, para t = 0.
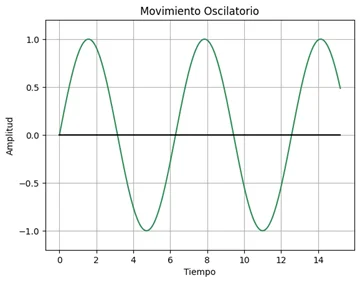
Volviendo a la suposición en el que el movimiento se realiza de manera unidimensional sobre el eje X, sin rozamiento, podemos contemplar el muelle con la masa unida a él como un sistema aislado.
La asunción de no existir rozamiento ni con el aire ni entre la superficie y la masa nos permite afirmar que se conserva la energía mecánica. Despreciando la masa del muelle, la energía cinética del movimiento se entiende como:
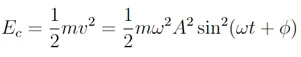
Y la energía potencial elástica como:
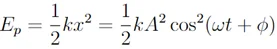
Quizá te interese leer este artículo sobre...
¿Quieres conocer otras formaciones en ciencias? ¡Mira esta oferta de formaciones online de Euroinnova!


¡Muchas gracias!
Hemos recibido correctamente tus datos. En breve nos pondremos en contacto contigo.