que es la distribucion normal

Te ayudamos a elegir tu formación, pulsa aquí.

Índice

Euroinnova APP

¡Aprender online está a solo un click!

Consíguelo en el

App Store

DISPONIBLE EN

Google Play

¿Qué es la distribución normal?

La distribución normal nos permite crear modelos de muchísimas variables y fenómenos, como por ejemplo, la estatura de los habitantes de un país, la temperatura ambiental de una ciudad, los errores de medición y muchos otros fenómenos naturales, sociales y hasta psicológicos. Por ello, hoy vamos a revisar sus características y los ejemplos que nos aclaren lo que es la distribución normal. ¡Acompáñanos!

La distribución normal, denominada también distribución gaussiana, es la que se utiliza más comúnmente en estadística, es un modelo que aproxima el valor de una variable aleatoria a una situación ideal, dependiendo de la media y la desviación típica (desviación estándar). ¿Quieres aprender más sobre esto? Entonces, continúa leyendo hasta el final para aprender más.

¿Qué encontrarás aquí?

1. ¿Qué es la distribución normal?
1.1. Características de la distribución normal
1.2. Importancia de la distribución normal
1.3. Ejemplos de distribución normal
1.4. Amplía tus conocimientos con Euroinnova
2. Cursos especializados en Estadística

Características de la distribución normal

Tiene forma de campana. Esto caracteriza a lo que es la distribución normal.
Puede tomar cualquier valor (de menos infinito a más infinito) es decir, utiliza variables cuantitativas continuas.
Es una distribución simétrica.
Es asintótica, es decir sus extremos nunca tocan el eje horizontal, cuyos valores tienden a infinito, esto es una regla empírica.
En el centro de la curva se encuentran la media, la mediana y la moda.
El área total bajo la curva representa el 100% de los casos.
Los elementos centrales del modelo son la media y la varianza.

Importancia de la distribución normal

Al conocer qué es la distribución normal podemos decir que su importancia se debe a tres razones fundamentales:

Un gran número de fenómenos reales se pueden modelizar con esta función gaussiana, tal es el caso de las características cuantitativas de casi todas las grandes poblaciones.
Muchas de las distribuciones de uso frecuente tienden a aproximarse a la distribución normal bajo ciertas condiciones.
En virtud del Teorema Central del Límite, todas aquellas variables que puedan considerarse causadas por un gran número de pequeños efectos (como pueden ser los errores de observación) tienden a distribuirse con una partición normal.

Ejemplos de distribución normal

Lo que es la distribución normal es un término que quizás no es sencillo de comprender o asimilar, la mejor forma de entenderlo es a través de ejemplos:

La estatura: Pensemos en la estatura de todas las mujeres portuguesas, dicha altura sigue una distribución normal. La estatura de la mayoría de mujeres estará cerca de la estatura media, podemos decir entonces que la altura media portuguesa es de 163 centímetros en las mujeres. Por otro lado, un número similar de mujeres serán un poco más altas y un poco más bajas que 163cm; sólo unas pocas serán mucho más altas o mucho más bajas.
Efectos de un fármaco: Cuando vamos a tomar alguna medicina podemos observar que la dosis de medicamento debe contener la medida exacta de principio activo para que éste pueda ser eficaz, efectivo y seguro para el paciente, para lograr esto se utiliza la distribución normal y otras fórmulas matemáticas que puedes conocer ingresando a Wikimedia Commons.
Puntuación de los estudiantes: Con la distribución normal no interesa tanto que los alumnos evaluados demuestren dominio de ciertos objetivos predeterminados, sino que interesa hacer una selección de los alumnos que, en relación con el grupo evaluado, demuestren ser los mejores en los ejercicios resueltos. Con esto podemos apreciar que a nivel estadístico existen diversas formas de evaluar aprendizajes.

Como verás la distribución normal está presente en nuestra vida diaria, sin embargo es un tema del cual se derivan otras aplicaciones que implican un estudio más profundo para poder entenderlo, para ello podemos ofrecerte opciones de estudio que te presentaremos a continuación.

Amplía tus conocimientos con Euroinnova

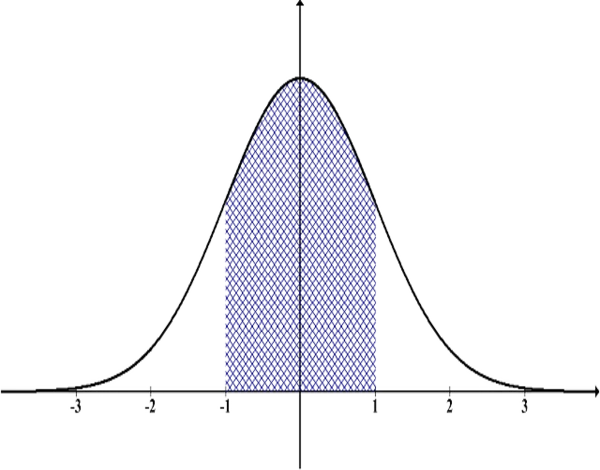
Si quieres ampliar tus conocimientos sobre lo que es la distribución normal, en Euroinnova la Escuela de Negocios especialista en formación vía online te invitamos a nuestro portal donde encontrarás mas de 19.000 cursos. Si tu interés está centrado en lo relacionado con la estadística te recomendamos ampliamente el Curso Básico de Estadística para Ciencias Sociales, el cual brinda conocimientos ideales a aquellos profesionales que quieran realizar un análisis estadístico de los fenómenos sociales.